- オームの法則の解法ポイントを教えて!
- オームの法則の問題って毎回出題されているのは本当?
オームの法則は電気の超基本。そして、電線の許容電流と同じくらいオームの法則の問題は電気工事士2種筆記試験ではほぼ毎回出題されます。計算が苦手な方でも比較的簡単に解ける問題ばかりなので、オススメの分野です。

この記事では、オームの法則が重要な問題であること、そして解法のポイントを把握することができます。この記事を読むことで、筆記試験対策の計算ポイントをサクッと理解できます。
オーム法則を使って解く問題は手順のほぼ1種類!少し応用も混ざるが、重要事項をきっちり押さえて置くことで、ほぼ問題は解けます。
毎回出題されるオームの法則の問題とは

令和4年(上期「午前/午後」)の2回、令和3年(上期「午前/午後」・下期「午前/午後」)の合計4回、令和2年の2回、令和元年の2回の合計10回の過去問を調べました。結果、毎年同じような問題と選択肢で構成されています。
| 出題年度 | 問題番号 | 問題文 | 回路図 | 回答群 | 備考 |
| 令和4年 (上期午前) | 1 | 図のような回路で,電流計 Aの値が1 Aを示した。このときの電圧計Vの指示値[V]は。 |  | イ.16 ロ.32 ハ.40 ニ.48 | 令和3年(下期午後) と全く同じ問題! |
| 令和4年 (上期午後) | 1 | 図のような回路で,スイッチSを閉じたとき,ab端子間の電圧[V]は。 |  | イ.30 ロ.40 ハ.50 ニ.60 | 令和3年(上期午前) と全く同じ問題! |
| 令和3年 (下期午前) | 1 | 図のような回路で、スイッチS1を閉じ、スイッチS2を開いたときの、端子a−b間の合成抵抗[Ω]は。 |  | イ.45 ロ.60 ハ.75 ニ.120 | |
| 令和3年 (下期午後) | 1 | 図のような回路で、電流計「A」の値が2Aを示した。このときの電圧計「V」の指示値[V]は。 |  | イ.16 ロ.32 ハ.40 ニ.48 | |
| 令和3年 (上期午後) | 1 | 図のような回路で、8Ωの抵抗での消費電力[W]は。 |  | イ.200 ロ.800 ハ.1200 ニ.2000 | ここだけ 少し特殊な問題 |
| 令和3年 (上期午前) | 1 | 図のような回路で、スイッチSを閉じたとき、a-b端子間の電圧[V]は。 |  | イ.30 ロ.40 ハ.50 ニ.60 | |
| 令和2年 (下期午前) | 1 | 図のような直流回路に流れる電流I[A]は。 |  | イ.1 ロ.2 ハ.4 ニ.8 | |
| 令和2年 (下期午後) | 1 | 図のような直流回路で、a−b間の電圧[V]は。 |  | イ.10 ロ.20 ハ.30 ニ.40 | |
| 令和元年 (上期) | 1 | 図のような回路で、スイッチSを閉じたとき、a−b間の電圧[V]は。 |  | イ.30 ロ.40 ハ.50 ニ.60 | |
| 令和元年 (下期) | 1 | 図のような回路で、端子a – b間の合成抵抗[ Ω ]は。 |  | イ.1 ロ.2 ハ.3 ニ.4 |

問題番号までそろっているのは驚いたね!基本的には電圧[V]か抵抗[Ω]を求める問題が多いね!令和4年もバッチリ出題されていたね!
直近4年で毎回出題されているオームの法則の問題。電気の基礎であり、確実に1問正解をもぎとることでより合格に近づきます。計算分野でもオームの法則は法則性が高いので、勉強しやすいです。
オームの法則の必須問題

必須問題に関係する知識を一挙にまとめていきます。
必須問題
図のような直流回路に流れる電流I[A]は。
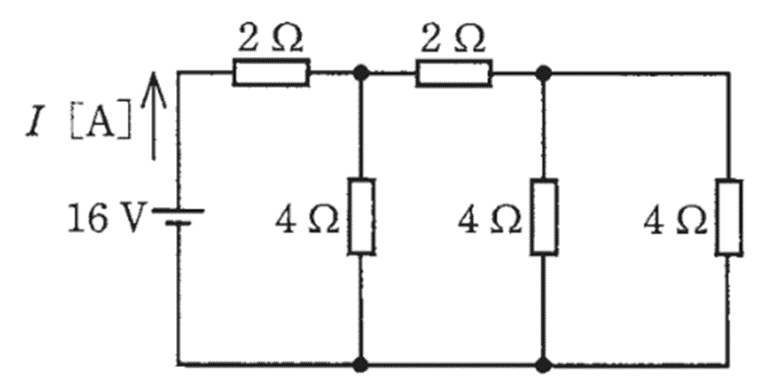
選択肢:イ.1 ロ.2 ハ.4 ニ.8
解答・解説
解答
- 解答:ハの4[A]
解説
オームの法則が絡む問題は、基本の解法がパターンが決まっています。
- 回路を見て電気の流れる通り道を確認する。
- 合成抵抗を求める。
- オームの法則を使用する。
オームの法則
まずはオームの法則です。
公式はこちらです。
公式チェックポイント
V[電圧:V] = I[電流:A] × R[抵抗:Ω]
I[電流:A] = V[電圧:V] ÷ R[抵抗:Ω]
R[抵抗:Ω] = V[電圧:V] ÷ I[電流:A]
よく小学生の時に学習した「は・じ・き」に習って覚えたり、滑り台・水車などで電気を流れるイメージでよく覚えたりします。

計算が苦手な方でもイメージで覚えれば解答しやすいよ!
合成抵抗
次は合成抵抗です。
公式はこちらです。
少し並列が難しいですが、まずは覚えましょう。
- 抵抗が直列に接続されている場合(直列接続)
- R[Ω] = R1 + R2
- 抵抗が並列に接続されている場合(並列接続)
- 1/R = 1/R1 + 1/R2
ここから、Rを求めます。
1/R = ( R1 + R2 ) ÷ ( R1 × R2 )
ここから逆数を取ります。
R[Ω] = ( R1 × R2 ) ÷ ( R1 + R2 )

2つの公式は確実に覚えておいてね!
この2つの式だけで確実に点数が稼げるね!
回答
合成抵抗R[Ω]=4[Ω]
電流I[A]=16[V] ÷ 4[Ω] = 4[A]
合成抵抗とオームの法則の公式を覚えているだけで、解くことができます。
よって、回答は「ハ.4A」となります。
周辺知識
もう一つだけ追加で覚えておいた方がよい知識があります。

関連する知識は一緒に暗記した方が覚えやすいので、一気に覚えてしまおう!
電力・電力量の公式は次の通りです。
オームの法則に出てきた「電圧[V]、電流[A]、抵抗[Ω]」を使って式を作ることができます。
基本の公式は次の通りです。
P[電力:W] = V[電圧:V] × I[電流:A]
この基本式以外にもオームの法則「V=I×R」を使えば、色々な式に変換できます。
チェックポイント
電力:P[W] = V × I = I2 × R = V2 ÷ R
電力量:W[W・s] = P[W] × t[秒:s]
すべて電力を求めることができます。

電力[W]に時間をかけ合わせることで電気をどの程度消費したかわかる「電力量」を求められるよ!
次の問題も周辺知識だけで十分に解けます。
図のような回路で、8Ωの抵抗での消費電力[W]は。
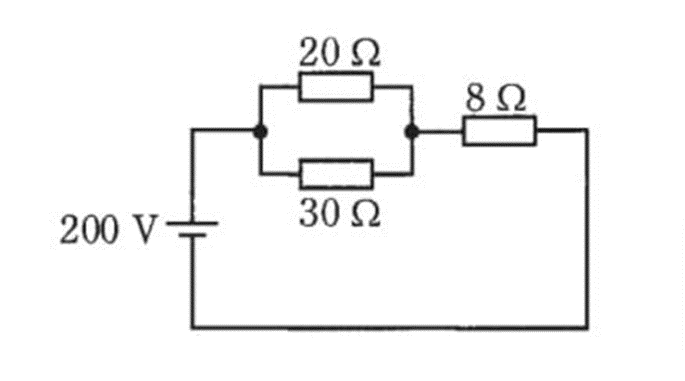
選択肢
イ.200
ロ.800
ハ.1200
ニ.2000
解説
電気回路をみて解答方針を考えます。
今回は「合成抵抗を求める」⇒「回路全体の電流を求める」⇒「電力の公式に当てはめて」解答をだす、という方針で今回は進めます。
まずは合成抵抗を求めます。
R=(20×30)÷(20+30)+8=12+8=20[Ω]
回路全体の電流を求めます。
I[A]=200[V]÷20[Ω]=10A
8Ωの抵抗の電力は、電力の公式にあてはめます。
P[W]=I2×R=102[A]×8[Ω]=100[A]×8[Ω]=800[W]
よって答えは、「ロ.800[W]」となります。

基本の解き方にほぼ習って解けることがわかったね!
電線の許容電流と同じでオームの法則に関する問題も覚える量が少ない!まずはここから公式を暗記して確実に得点源にしよう!
最後に:オームの法則の解法ポイントを押さえて最短合格しよう!

ポイントをまとめておきます。

オームの法則の解法はほぼ1パターンで毎年出題されています。計算問題の中でもかなりおいしい問題です。ぜひ得点源になるように頑張ってください。
その他に出題傾向が高い問題は次の記事でまとめています。ぜひ読んで効率よく合格を目指してください。






